1. f[40]={0,1}
数组赋值:只赋值前两个的话,剩余的自动为0
2.先要自己写出斐波拉契数列判断一下应该要多少个斐波拉契数样例,第39项已经超样例数500了,所以够用
3.就是把一个数字拆分成斐波拉契数列里的数的和嘛,但是要从数列中最大的数找,找到了就标注二进制数组中为1
4.输出时也是以高位开始,但是高位开始的就会有0不标记的,不作数,先排除,遇到第一个不为0的再把其后面的输出
#include <iostream>
using namespace std;
int main()
{
int f[40]={0,1}, b[40], n, m;
for (int i = 2; i < 40; i++)
{
f[i] = f[i - 1] + f[i - 2];
}
cin >> n;
while (n--)
{
cin >> m;
cout << m << " = ";
for (int i = 39; i >= 0; --i)
{
if (f[i] <= m)
{
b[i] = 1;
m -= f[i];
}
else b[i] = 0;
}
int j = 39;
while (!b[j]) --j;
while (j >=2) cout << b[j--];
cout << " (fib)" << endl;
}
return 0;
}


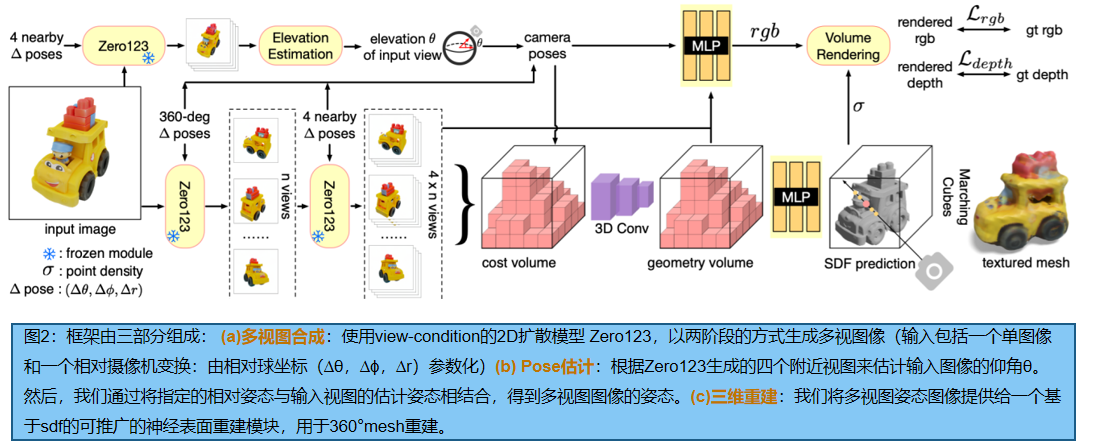
![[Mongodb 5.0]聚合操作](https://img-blog.csdnimg.cn/e214570cfad444b78722a55f60d92d26.png)